Producto de Matrices
Consideremos la matriz de dimensión y la matriz de dimensión . Notemos que el número de columnas de coincide con el número de filas de .
Bajo estas condiciones, llamamos producto (matricial) de las matrices y , y lo representamos por ó simplemente , a la matriz que tiene en el elemento de la fila y la columna el resultado del producto escalar del vector formado por la fila de la matriz por el vector formado por la columna de la matriz .
La matriz es de dimensión .
Ejemplo 1
Calculemos el producto de matrices
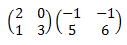
Llamaremos A a la matriz de la izquierda y B a la de la derecha. Estas matrices son de dimensiones 2x2, por lo que podemos calcular el producto AB que será una matriz de dimensión 2x2.
Llamaremos A a la matriz de la izquierda y B a la de la derecha. Estas matrices son de dimensiones 2x2, por lo que podemos calcular el producto AB que será una matriz de dimensión 2x2.
- El elemento de la fila 1 y la columna 1 de AB es el producto escalar de los vectores fila 1 de A y columna 1 de B
- El elemento de la fila 1 y la columna 2 de AB es el producto escalar de los vectores fila 1 de A y columna 2 de B
- El elemento de la fila 2 y la columna 1 de AB es el producto escalar de los vectores fila 2 de A y columna 1 de B
- El elemento de la fila 2 y la columna 2 de AB es el producto escalar de los vectores fila 2 de A y columna 2 de B
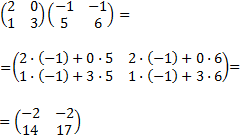
Más ejemplos del producto de matrices
Más ejemplos del producto de matricesPropiedades del producto de matrices
Comentaremos las propiedades inmediatas de la definición (no las demostraremos).
- El producto de matrices no es conmutativo. Esto quiere decir que la matriz producto puede ser distinta de la matriz producto . De hecho, si las matrices son rectangulares (no cuadradas), entonces uno de los dos productos no puede calcularse (no está definido). En el ejemplo anterior, el producto BA es distinto de AB.
- La matriz identidad es el elemento neutro (por la izquierda, por la derecha o por ambos lados) del producto de matrices. La matriz identidad de dimensión n, I, es la matriz de dimensión formada por ceros excepto la diagonal, que está formada por unos. Ejemplos de matrices identidades:
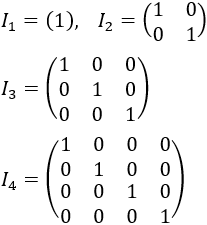
- Consideremos que la dimensión de la matriz identidad I es la adecuada para poder multiplicarse con la matriz A. Entonces, IA=A y AI=A. La matriz identidad es como el número 1 en el producto de los números reales.
- El producto de matrices diagonales es una matriz diagonal.
- El producto de matrices triangulares superiores (inferiores) es una matriz triangular superior (inferior).