さらに環
このワークシートはMath by Codeの一部です。
前回は、ガウス整数が、ずっこけているどころか、整数でできることが全部できた。
剰余、互除法、素因数分解。
すばらしい整数であることがわかった。
整数という環に、iを添付すること環を拡張したものとも言える。
添付するものを変えて、いろんな環を作ってみよう。
アイゼンシュタイン整数の基底
1.アイゼンシュタイン整数
<アイゼンシュタイン整数も環だ>
アイゼンシュタイン整数はiの代わりにω=(-1+√3i)/2を整数に添付したものだ。
これをZ[ω]とかこう。
ω3=1, ω3-1=(ω-1)(ω2+ω+1)=0から、ω2=-1-ωを確認しておく。
2項演算+について、<Z[ω]、+>は可換群だ。
2項演算×について、<Z[ω]、×>は可換なモノイドだね。
+、×についての分配法則が成り立つ。
a,b,c∈Z[ω]なら(a+b)×c=a×c+b×c
<ノルム>
アイゼンシュタイン整数a=x+yωの原点からの距離の2乗をノルムという。
ノルムはN(a)=|a|2と書く。N(a)は非負であり、N(a)=0となるのは、a=0に限る。
N(a)=|x+yω|2=|x+y(-1+√3i)/2|2=|(x-y/2)+i√3y/2|2=(x-y/2)2+(√3y/2)2=x2+y2-xy
途中計算は略するが、N(ab)=N(a)N(b)。
単元のノルム=1とすると、x2+y2-xy=(x-y/2)2+(√3y/2)2=1
(2x-y)2+3y2=4から、(2x-y,y)=(2,0),(-2,0),(1,1),(1,-1),(-1,1),(-1,-1)
(x,y)=(1,0),(-1,0),(0,1),(0,-1),(1,1),(-1,-1)だから、単元a=1, -1, ω, -ω, 1+ω, -1-ωの6個。
整数aの単元倍をした数を同伴数という。
<倍元>
整数x=a+bωの倍元どうしはどんな関係になるだろうか。
xに任意の整数y=m+nωをかけたものxy=x(m+nω)=m(x)+n(ωx)となる。
だから、x=a+bωとωx=ω(a+bω)の一次結合といえるね。
ω3=1なのだからωは(1,0)を原点を中心に120度回転する働きがある。
ベクトルのように、複素数をたし算すると、1+ωが、1とωを2辺とする対角線だから、
1を60度回転した位置にある。
1,1+ω,ωをω2倍すると、-1-ω,-ω,1となる。結局、この6点は正六角形の頂点になる。
これをアイゼンシュタイン格子点と呼ぼう。単元と同じになっているのがわかるね。
ωを外してiで計算すると、複素平面での実軸、虚軸での位置づけになってしまう。
アイゼンシュタイン整数を扱いやすくするには、
実軸と、原点を中心に120度反時計回りに回転したω軸の2軸という斜交座標系でイメージしよう。
この2軸の基底ベクトル1とωのx,y倍が(x,y)=x+yωだとしてみる。
実際は2軸の作る角を2等分する1+ω軸の3軸目を書いておくと、正三角形の作る格子点の集合体が
アイゼンシュタイン整数になるね。
x=a+bωを120度回転したωx=aω+bω2=b(-1-ω)+aω=-b+(a-b)ωと原点が作るひし形(
正三角形を2つくっつけた)4頂点を平行移動した格子点がx=a+bωの倍数となるね。
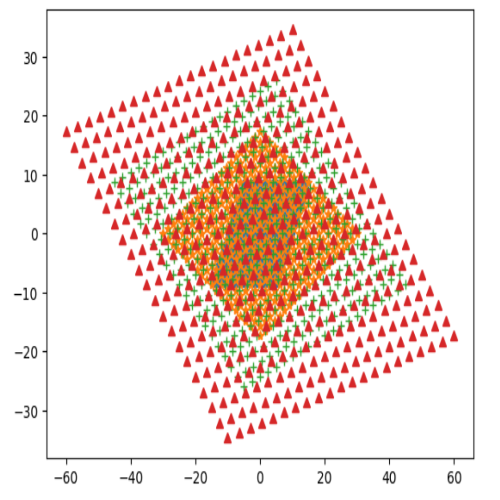
質問:アイゼンシュタイン整数1+ω,2+ω,3+ω,4+ωの倍元を描くにはどうしましょうか。
ωをcomplex関数で作っておき、x+yωを返す関数ome(x,y)を作っておけば、
iがωに変わっただけというようにお手軽に倍元を視覚化できますね。
(1,ω)座標系に戻す必要がないので、ガウス平面の座標系(1,i)で計算してしまってかまわないね。
import numpy as np
import matplotlib.pyplot as plt
def ome(x,y):
ω = complex(-1/2,3**0.5/2)
return x + y*ω
m = [ome(1,1), ome(2,1), ome(3 ,1), ome(4 ,1)]
fig = ['.','*','+','^']
for num in range(len(m)):
bai=[m[num]*ome(x,y) for x in range(-10,11) for y in range(-10,11)]
xs=[c.real for c in bai]
ys=[c.imag for c in bai]
plt.plot(xs,ys,fig[num])
[OUT]
<割り算の商と余り>
アイゼンシュタイン整数x=a+bωの高さH(x)をノルムN(x)=a2+b2-abで定義してみよう。
N(x)は非負整数だ。
・H(x)=0の核はx=0に限る。
・非ゼロのx,y∈Z[ω]でH(xy)>=H(x)。=はyが単元なら、60度の倍数回転だから同じノルムだ。
議論を見やすくするために、複素数の基底を(1,i)系ではなく、(1,ω)系で演算法則を作っておこう。
x=a+bω、y=c+dω、ω2=-1-ω
和差x+y=(a,b)+(c,d)=(a+c,b+d), x−y=(ab)-(c,d)=(a-b,c-d)
積xy=(a,b)(c,d)
=ac+bdω2+(ad+bc)=ac+(-bd-bdω)+(ad-bc)ω=(ac-bd)+(ad+bc-bd)ω
=(ac-bd, ad+bc-bd)
√3iをカンタンのためにrとすると、2ω=-1+rとなり、r2=-3 , r=2ω+1
商x/y=(a,b)/(c,d)
=((2a-b)+br))/((2c-d)+dr)={((2a-b)+br))((2c-d)-dr)}/{((2c-d)+dr)((2c-d)-dr)}
{(2a-b)(2c-d) + (-(2a-b)d+(2c-d)b)r - bdr2)((2c-d)+r)}/((2c-d)2-(dr)2)
分子=(4ac-2bc-2ad+bd+3bd)+(-2ad+bd+2bc-bd)r=2(2ac-ad-bc+2bd)+2(-ad+bc)r
分母=4c2+d2-4cd+3d2=4(c2+d2-cd)
だから、x/y={(2ac-ad-bc+2bd)+(-ad+bc)r}/2(c2+d2-cd)
={(2ac-ad-bc+2bd)+(-ad+bc)(2ω+1)}/2(c2+d2-cd)
={(2ac-ad-bc+2bd+(-ad+bc))+(-ad+bc)2ω}/2(c2+d2-cd)
=(2ac-2ad+2bd)/2(c2+d2-cd) +ω(-ad+bc)/(c2+d2-cd)
=(ac-ad+bd)/(c2+d2-cd)+ω(bc-ad)/(c2+d2-cd)
x/y=(a,b)/(c,d) =1/N(y) (ac-ad+bd, bc -ad)
(1,ω)基底の斜交座標で表すと複雑に見えるが、そのつど(1,i)基底から戻すよりはよいでしょう。
・どの非ゼロのx、y∈Z[ω]に対しても、q,r∈Z[ω]があり、y=qx+r で、0<=H(r)<H(x)となる最小のrがある
両辺をxで割ると、y/x= q + r/x, H(r/x)<1 z= y/x=a+bω(a,b∈R)。
zがアイゼンシュタイン格子点のとき、つまり、z∈Z[ω]なら、H(r/x)<1だから、r=0。
zが格子点でなく、近い格子点の1つがcならH(z-c)<1。商をcとするときの余りをrとすると、
z=y/x, xz=yから、r=y-cx=xz-cx=x(z-c)だから、N(r)=N(x)N(z-c)<N(x)
(例)
y=7+5ω, x=5+ω なら、N(x)=52+12-5*1=25+1-5=21
y/x=(7+5ω)/(5+ω)=1/21(7*5-7*1+5*1, 5*5-7*1)=1/21(33, 18)≒1.57+0.86ω
y/xに近い格子点が2+ωならq=2+ω。r=y-qx=7+5ω-(5-ω)(2+ω)=-2-ω
N(x)=21, N(r)=3だから、rは余りとなる。y÷xの商は2+ω, 余りは-2-ω
質問:アイゼンシュタイン整数どうしの割り算の商・余りはコードでどうやれば出せますか。
あたかも、2つの仮分数の四則計算を2成分の演算として定義できるように、
複素数の基底を(1,ω)とした2成分数の演算として四則計算をルール化してみよう。
最近の格子点を探すときだけ、(1,i)基底で計算すると、
コードが見やすくなるね。
#アイゼンシュタイン整数の演算
#複素数の基底を(1,i)ではなく(1,ω)で四則演算する。
[IN]Python
#==========================================
import numpy as np
def ome(x,y):#最近格子点を探すときだけ必要になる。
ω = complex(-1/2,3**0.5/2)
return x + y*ω
def Norm(x):
return x[0]**2 + x[1]**2 - x[0]*x[1]
def add(x,y):
return (x[0] + y[0], x[1] + y[1])
def diff(x,y):
return (x[0] - y[0], x[1] - y[1])
def multi(x,y):
return (x[0]*y[0] - x[1]*y[1], x[0]*y[1] + x[1]*y[0] - x[1]*y[1])
def quot(x,y):
nrm = Norm(y)
return ((x[0]*y[0] - x[0]*y[1] + x[1]*y[1])/nrm,(x[1]*y[0] - x[0]*y[1])/nrm )
def diviz(y, x):
A = (y[0],y[1])
B = (x[0],x[1])
qC = quot(A,B)
print(f"A/B = {A}/{B} = {qC}")
real ,omega = qC[0],qC[1]
xl, yB = int(real),int(omega)
xr, yT = xl + 1, yB + 1
grid = [(xl,yB),(xl,yT),(xr,yB),(xr,yT)]
dists = np.array([abs(ome(k[0],k[1])-ome(real,omega)) for k in grid])
indx = dists.argmin()
Q = grid[indx]
R = diff( A , multi(B , Q))
print(f"{A} = {B}×{Q} + {R}")
return A,B,Q,R
y = (7,5)
x = (5,1)
diviz(y,x)
[OUT]
A/B = (7, 5)/(5, 1) = (1.5714285714285714, 0.8571428571428571)
(7, 5) = (5, 1)×(2, 1) + (-2, -1)
<その先へ>
3+4ωは素元か?
3+4ω=abとすると、N(3+4ω)=N(a)N(b)
N(3+4i)=32+42-3*4=25-12=13だから、a,bが単元でないなら、N(a)かN(b)が13になる。
だから、3+4ωは素元だ。
このようにノルムN(x)=a2+b2-abが素数ならばアイゼンシュタイン素元になるね。
ノルムが素数でなくてもアイゼンシュタイン素元になるものもある。
たとえば、2、5などがそうだ。
また、割り算の商と余りが出せるということは、ユークリッドの互除法で最大公約元を求めることもできる。そして、素因子分解の一意性も導くことができるでしょう。
アイゼンシュタイン整数は、ガウス整数よりも扱いにくかったけれど、
ユークリッド整域という位置づけ自体では同等だということがわかるね。
2.円分整数
<円分体と円分整数>
円分方程式zn=1の解は、z=1を通る単位円に内接する正n角形の頂点に一致することは有名だ。
zは1のn乗根であり、z=e2πik/n(kは0以上n-1以下のk個)=cos(2πk/n)+i sin(2πk/n)
ただし、z=e2πi/n=cos(2π/n)+i sin(2π/n)として、k=1のときのzをζ(ジータ)とかくと、
ζと1の作る角はちょうど円のn等分の1つ分になっている。
ここからは、面倒なのでζをzとかくことにする。
これがn個の解の生成元になる。k=0またはnのときzk=1で、それ以外は1以外の複素数になる。
だから、1以外の複素数解はをzk(kは1以上n-1の整数)とかけるね。
有理数Qにzkを添付した複素数全体Q(z1,z2,...,zn-1)はz1,z2,...,zn-1を含む最小の体で円分体という。
1の奇素数p乗根のzのp-1次の整数係数の多項式の形の複素数を円分整数という。
この場合もZ[z]を含む最小の体Q[z]を円分体という。
Zにi、ωを添付したガウス整数Z[i]、アイゼンシュタイン整数のZ[ω]と同様に、
Zにzを添付した円分整数はZ[z]と書く。(正式にはZ[ζ]とかくのだが。。。)
ただし,zは累乗の指数の違いによって同類にできないから、zの整数係数の多項式で元を表そう。
これをZ[z]とかこう。
zp=1, zp-1=-(1+z+.....+zp-2)次元下げを確認しておく。
(zのp-1次の多項式は次元下げによって、p-2次式で一意的にあらわすこともできる。)
だから、たとえば1の5乗根の円分整数はzの3次式として設定することもできる。
2項演算+について、<Z[z]、+>は可換群だ。
2項演算×について、<Z[z]、×>は可換なモノイドだね。
+、×についての分配法則が成り立つ。
a,b,c∈Z[z]なら(a+b)×c=a×c+b×c
<ノルム>
1のp=5乗根の円分整数の要素はz=e2πi/5の3次式で一意に表すことができる。
形式的には4次多項式で表すことできる。ノルムは多項式のzに順次zからzp-1乗を代入した積。
a=f(z)=a0+a1z+a2z2+a3z3+a4z4 係数ai∈{-2,-1,0,1,2}
ノルムN(a)=f(z)f(z2)f(z3)f(z4)となる。
a=f(z), b=g(z)なら、
N(ab)=N(f(a)g(b))=(f(z)g(z)f(z2)g(z2)f(z3)g(z3)f(z4)g(z4))=(f(z)f(z2)f(z3)f(z4)g(z)g(z2)g(z3)g(z4))
N(a)N(b)
(例)
5乗根の円分整数a=f(z)=1+2z3のノルム
N(a)=f(z)f(z2)f(z3)f(z4)=(1+2z3)(1+2z6)(1+2z9)(1+2z12)=(1+2z3)(1+2z1)(1+2z4)(1+2z2)
=(1+2z3)(1+2z2)(1+2z1)(1+2z4)=(1+2(z3+z2)+4)(1+2(z1+z4)+4)
=(5+2(z3+z2))(5+2(z1+z4))=25+10(z3+z2+z1+z4)+4(z4+z7+z3+z6)
=25+10(-1)+4(z4+z2+z3+z1)=25-(10+4)=11 (z4=-(1+z+z2+z3)で次元下げ)
ガウス整数のときのように、ノルムに関連付けて円分整数の素元の特徴を探る可能性が出てくる。
また、ノルムの計算公式を作ることで、考察しやすくなるでしょう。
クンマーさんは、「奇素数pの円分整数は素元分解の一意性が持てる」かもという方向で研究をしていたけど、それができない奇素数pが見つかり、夢は挫折してしまったと言われている。
しかし、その副産物として、理想的複素数とか、正則な素数など、そのあとの数学者の研究につながる成果を残している。
3.もっと環
<自明な環>
単純すぎて、当たり前すぎる環があることに気づいてますか?
ゼロ環です。
0+0=0
0×0=0だから、
0は加法のゼロ元であり、
乗法のイチ元でもあるから
{0}は立派は環です。
つまらないですね。
<単元群>
どんな環にも単元があります。
UV=1となるU、Vです。単元だけで乗法について群ができます。
(例)
Zの単元群は{1,-1}。
Z[i]の単元群は{1,-1,i,-i}
Z[ω]の単元群は{1,-1,ω,-ω,1+ω,-1-ω}。
環は整数のしくみを素材を変えて広げたものだね。
かけ算とわり算がどうなるかで、環、整域、ユークリッド整域、さらには体に成れたりもする。
そこを詳しくしらべると、さらに環の仲間をふやせそうだね。