Dudeney: Choosing a Site in an Isosceles Estate
Henry Ernest Dudeney (1857-1930)
There are already 16 activities in the GeoGebra resources online pages with the tag “dudeney”, most of them illustrating HE Dudeney’s famous Haberdasher’s Puzzle. My own one, posted 10 September, 2011 is entitled Dudeney's dissection of a scalene triangle to form a square.
In these COVID times, I turn again to HED’s Puzzles and Curious Problems (1931), the copy that belonged to my paternal grandfather. How can GeoGebra be used in interesting ways to illustrate some of the problems therein?
Problem 328, Choosing a Site:
A man bought an estate enclosed by three straight roads forming an equilateral triangle, as shown in the illustration. Now, he wished to build a house somewhere on the estate so that if he should have a straight carriage-drive made from the front to each of the three roads he might be put to the least expense. The diagram shows one such position. Where should he build the house?
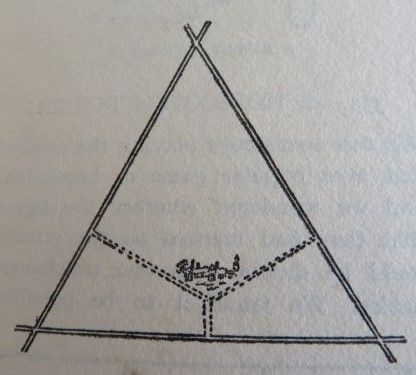
HED’s solution is as follows:
This was a little jest. He may build wherever he pleases, for if perpendiculars are drawn to the sides of an equilateral triangle from any point in the triangle, their united length will be equal to the altitude of the triangle.
How is HED’s assertion evident?
This applet illustrates the more general case for choosing the man’s site, given an isosceles triangle. The sides b and c each have length 4, while a has length 4q. Initially q = 1, so this is the equilateral case as set by HED. The equilateral triangle is divided into three triangles (separated by the dotted lines), each with base 4 and with altitude shown in green. The house is to be located at the green point (where the altitudes
meet). This point can be moved (left to right), and up and down (by moving the blue point on side b). The length of the roads is or approximately 3.46, and appears to be invariant (that is independent of the position of the house).
The justification is simple. Since each of the three triangles has base 4, each has area equal to twice its altitude, so the sum of the three areas is just twice the sum of the altitudes which must equal the area of the equilateral triangle (twice its altitude). Thus HED’s assertion is made evident – QED!
Generalization
Now it is interesting to generalize the scenario posed by HED. What if the triangle is isosceles?
Choose q = 1.25, say, so that the triangle now has base 5 units with the other sides each 4. Moving the green point to the left or right does not change the length of the roads, but moving it up or down does. Thus each horizontal (dashed) line is a ‘contour’ associated with a constant length, yet varying between 3.12 and 3.90 as the position moves from top to bottom (the lower value being , the upper is 25% greater).
Other generalisations of Problem 328, supported by GeoGebra, are in preparation. In the meantime, enjoy exploring Choosing a Site in an Isosceles Estate …