Coordinate Systems
- Author:
- Judith Hilinski
- Topic:
- Geometry
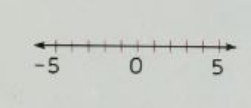
According to the Ruler Postulate, the points on a line can be numbered so that to every point there is matched number called its coordinate.
A line numbered in this way is a one dimensional coordinate system (number line).
One Dimensional Coordinate System
If two lines are numbered according to the Ruler Postulate are perpendicular to one another (as shown in the figure below) the number lines become the axes of a two dimensional coordinate system.
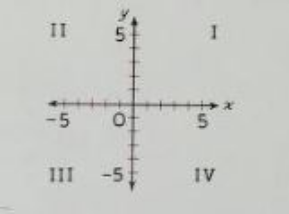
The axes are labeled x and y, and the point in which they intersect, zero on each axis, is labeled with a capital O and is the origin of the coordinate system.
The axes separate the plane that contains them into four parts (quadrants). The quadrants are identified by Roman numerals.
| Roman Numeral | Counting Number |
| I | 1 |
| II | 2 |
| III | 3 |
| IV | 4 |
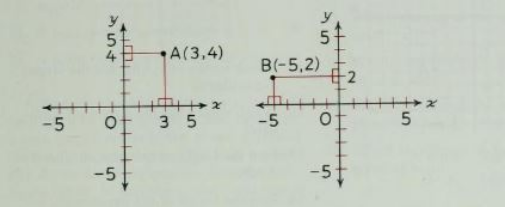
To find the coordinates of any given point on a coordinate plane, locate the point and draw a perpendicular line from the point to the x axis. That is the point's x coordinate.
Return to the same point and draw a perpendicular line from the point to the y axis. That is the point's y coordinate.
How to find the coordinates of a point
Definitions
The x-coordinate of a point is the number located on the x-axis (back and forth line)
The y-coordinate of a point is the number located on the y-axis (up and down line)
The coordinates of a point are written in parentheses and separated by a comma
The x coordinate is ALWAYS listed first (x,y)
The following exercises refer to the figure below.
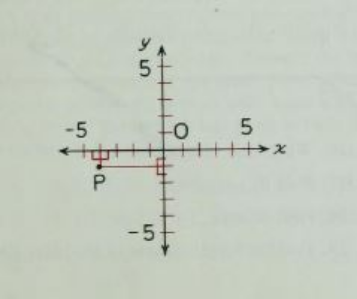
Question 1
What are the lines labeled x and y called?
Question 2
What is the point labeled O called?
Question 3
Which quadrant is point P in?
Question 4
What is the x-coordinate of point P?
Question 5
What is the y-coordinate of point P?