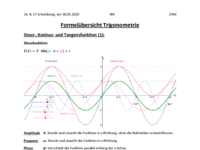
Eigenschaften der Winkelfunktionen
Verschiebe die Schieberegler, um damit die unten stehenden Fragen zu beantworten
Schreibe diese auch als Festigung in dein Heft.
Betrachte die Funktion f(x)=A∙sin(ω∙x+φ)+c genau und gib an, nach welchem Abstand auf der x-Achse sich die Funktion wiederholt (diesen Wert nennt man Periodenlänge)
Periodenlänge:
Welche Werte nimmt die Funktion f(x)=sin(x) an (Werte auf der y-Achse)
Wertemenge W=[ ; ]
Gib die Nullstellen der Sinusfunktion an (wenn möglich auch allgemein)
Nullstellen:
Verschiebe einzeln die Schieberegler der Parameter oder schalte die Animation (mit einem Klick auf den Play-Button in der linken Spalte) ein und beobachte und dokumentiere, wie sich die Funktion verändert.
Amplitude A:
Frequenz ω:
Phase φ:
Konstante c:
Zeichne in GeoGebra die Funktion g(x)=cos(x) (indem du auf den leeren Kreis neben der Funktion g(x) in der linken Spalte klickst).
Vergleiche die Sinus- mit der Kosinusfunktion (Stelle dazu die Schieberegler der Amplitude und der Frequenz wieder auf 1 und die der Phase und der Konstante auf 0) . Um welchen x-Wert sind sie verschoben?
Verschiebung: cos→sin: sin→cos: (Gib die Richtung mit Vorzeichen an)
Schalte die Funktion f(x)=sin(x) aus, indem du auf den vollen Kreis neben der Funktion f(x) in der linken Spalte klickst.
Sieh dir die Funktion g(x)=cos(x) genau an und gib an, nach welchem Abstand auf der x-Achse sich die Funktion wiederholt (diesen Wert nennt man Periodenlänge)
Periodenlänge:
Welche Werte nimmt die Funktion g(x)=cos(x) an (Werte auf der y-Achse)
Wertemenge W=[ ; ]
Gib die Nullstellen der Kosinusfunktion an (wenn möglich auch allgemein)
Nullstellen:
Schalte die Funktion g(x)=cos(x) aus, indem du auf den vollen Kreis neben der Funktion g(x) in der linken Spalte klickst.
Zeichne in GeoGebra die Funktion h(x)=tan(x) (indem du auf den leeren Kreis neben der Funktion h(x) in der linken Spalte klickst)
Sieh dir die Funktion genau an und gib an, nach welchem Abstand auf der x-Achse sich die Funktion wiederholt (diesen Wert nennt man Periodenlänge)
Periodenlänge:
Welche Werte nimmt die Funktion h(x)=tan(x) an (Werte auf der y-Achse)
Wertemenge W=[ ; ]
Gib die Nullstellen der Tangensfunktion an (wenn möglich auch allgemein)
Nullstellen:
Gib die Asymptoten der Tangensfunktion an (Horizontale, die die Funktion einschränkt)
Asymptoten:
Wenn du alles abgeschlossen hast, sieh dir die Datei: Winkelfunktionen Theorie an, um sie mit deinen Ergebnissen zu vergleichen.