Analytic Geometry in 3D
Using the construction Tools available in the 3D Graphics View Toolbar you can create geometric constructions in the  3D Graphics View with the mouse. Select any construction tool from the 3D Graphics View Toolbar and read the tooltip provided in the
3D Graphics View with the mouse. Select any construction tool from the 3D Graphics View Toolbar and read the tooltip provided in the  3D Graphics View in order to find out how to use the selected Tool.
Note: Any object you create in the
3D Graphics View in order to find out how to use the selected Tool.
Note: Any object you create in the  3D Graphics View also has an algebraic representation in the
3D Graphics View also has an algebraic representation in the  Algebra View and vice versa any analytic representation in the
Algebra View and vice versa any analytic representation in the  Algebra View has an graphical output in the
Algebra View has an graphical output in the  3D Graphics View.
Direct Input using the Input Bar
GeoGebra’s
3D Graphics View.
Direct Input using the Input Bar
GeoGebra’s  3D Graphics View supports points, vectors, lines, planes, and surfaces in a three-dimensional coordinate system. You may either use the Tools provided in the 3D Graphics View Toolbar, or directly enter the algebraic representation of these objects in the Input Bar or Input Field of the
3D Graphics View supports points, vectors, lines, planes, and surfaces in a three-dimensional coordinate system. You may either use the Tools provided in the 3D Graphics View Toolbar, or directly enter the algebraic representation of these objects in the Input Bar or Input Field of the  Algebra View (GeoGebra Web and Tablet Apps).
Example: Enter
Algebra View (GeoGebra Web and Tablet Apps).
Example: Enter 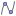 Algebra View in order to create a point in the three-dimensional coordinate system.
Example: Enter
Algebra View in order to create a point in the three-dimensional coordinate system.
Example: Enter  helps you to set up proper view direction.
Exercise:
Line in 3D space is represented parametrically, by one-parameter vector function X(t) = [x(t), y(t), z(t)].
Is the given line parallel to any coordinate axis or plane (x-axis, y-axis, z-axis, xy-plane, yz-plane, xy-plane)?
helps you to set up proper view direction.
Exercise:
Line in 3D space is represented parametrically, by one-parameter vector function X(t) = [x(t), y(t), z(t)].
Is the given line parallel to any coordinate axis or plane (x-axis, y-axis, z-axis, xy-plane, yz-plane, xy-plane)?
A=(5, -2, 1) into the Input Bar or Input Field of the z = - x - y in order to create the corresponding surface.
Furthermore, you may now create curves, planes, as well as arbitrary parametric surfaces.
Command Surface(x(s,t),y(s,t),z(s,t),s,0,1,t,-1,2)
create surface given by parametric notation X(s,t) = [x(s,t),y(s,t),z(s,t)]. Bounds (0, 1) and (-1, 2) determine the size of rendered part of surface.
Tool Rotate 3D Graphic View  helps you to set up proper view direction.
Exercise:
Line in 3D space is represented parametrically, by one-parameter vector function X(t) = [x(t), y(t), z(t)].
Is the given line parallel to any coordinate axis or plane (x-axis, y-axis, z-axis, xy-plane, yz-plane, xy-plane)?
helps you to set up proper view direction.
Exercise:
Line in 3D space is represented parametrically, by one-parameter vector function X(t) = [x(t), y(t), z(t)].
Is the given line parallel to any coordinate axis or plane (x-axis, y-axis, z-axis, xy-plane, yz-plane, xy-plane)?
- X(t) = (1+t, 2+t, 1+t)
Rewrite the vector in algebraic window. Investigate the position of line in the
 3D Graphics View.
Solution is evident from the parametric representation. Line is given by point A = (1,2,1) and vector u = (1,1,1). This vector is not parallel with any coordinate planes.
3D Graphics View.
Solution is evident from the parametric representation. Line is given by point A = (1,2,1) and vector u = (1,1,1). This vector is not parallel with any coordinate planes.
- Y(t) = (1 - t, 2 + t, 1) Direction vector v = (-1, 1, 0) is parallel with coordinate plane (xy).
Task 2 - Geotest 11103
Choose the proper entity (shape) in 3D which is expressed by the given equation or the parametric form.
- a(s,t) = (1 + 2s - t, 2 - s, 1)
Write command
Surface(1 + 2s - t, 2 - s, 1, s, -2, 3, t ,-5, 5)into the Input Bar of the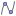 Algebra View. Bounds (-2, 3) and (-5, 5) and determine only the size of rendered part of plane. You can change them later in order to fit the illustrativ view.
Solution is evident from the parametric representation. All coordinates are linear function of two parameters. Two parametric linear object is plane. Missing parameter gives us reference about parallelity with coordinate axis. For instance, function for third coordinate z=1 doesn't contain both parameters s, t. That means, that plane a must be parallel with xy-plane.
Algebra View. Bounds (-2, 3) and (-5, 5) and determine only the size of rendered part of plane. You can change them later in order to fit the illustrativ view.
Solution is evident from the parametric representation. All coordinates are linear function of two parameters. Two parametric linear object is plane. Missing parameter gives us reference about parallelity with coordinate axis. For instance, function for third coordinate z=1 doesn't contain both parameters s, t. That means, that plane a must be parallel with xy-plane.
- x - y + 4 = 0
Enter
x - y + 4 = 0into the Input Bar of the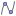 Algebra View. Object is depicted as line in pure Graphis window - intersection of plane and coordinate plane xy.
Algebra View. Object is depicted as line in pure Graphis window - intersection of plane and coordinate plane xy.  3D Graphics View gives the whole plane.
Linear equation F(x, y, z) = 0 always represents plane in 3D space. Missing parameter gives us reference about parallelity with coordinate axis. General equation x - y + 4 = 0 doesn't contain z. From that, plane is parallel with z-axis.
3D Graphics View gives the whole plane.
Linear equation F(x, y, z) = 0 always represents plane in 3D space. Missing parameter gives us reference about parallelity with coordinate axis. General equation x - y + 4 = 0 doesn't contain z. From that, plane is parallel with z-axis.