Unghi cu vârful în interiorul cercului
Pentru a realiza un unghi cu vârful în interiorul unui cerc, folosind Geogebra, urmăriți pașii:
1) Desenați un CERC cu raza de 3 unități de măsură: - Selectați pictograma 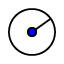 , apoi dați click pe sufrafața de lucru a ferestrei GeoGebra de mai jos și introduceți raza 3 în fereastra ce apare pe pagina principală.
Ați realizat un cerc de centru A și rază 3.
2) Desenați patru PUNCTE (B, C, D și E) pe cercul de centru A, folosind pictograma
, apoi dați click pe sufrafața de lucru a ferestrei GeoGebra de mai jos și introduceți raza 3 în fereastra ce apare pe pagina principală.
Ați realizat un cerc de centru A și rază 3.
2) Desenați patru PUNCTE (B, C, D și E) pe cercul de centru A, folosind pictograma  .
3) Trasați două DREPTE determinate de cele patru puncte, astfel încât acestea să fie concurente într-un punct aflat în interiorul cercului: - Faceți acest lucru selectând pictograma
.
3) Trasați două DREPTE determinate de cele patru puncte, astfel încât acestea să fie concurente într-un punct aflat în interiorul cercului: - Faceți acest lucru selectând pictograma 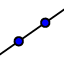 , apoi selectați câte două dintre punctele de pe cerc.
4) Notați PUNCTUL DE INTERSECȚIE al celor două drepte: - selectați pictograma
, apoi selectați câte două dintre punctele de pe cerc.
4) Notați PUNCTUL DE INTERSECȚIE al celor două drepte: - selectați pictograma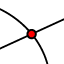 , apoi selectați cele două drepte concurente. Veți constata apariția unui punct F.
5) Aflați MĂSURA UNGHIULUI determinat de cele două drepte: - selectați pictograma
, apoi selectați cele două drepte concurente. Veți constata apariția unui punct F.
5) Aflați MĂSURA UNGHIULUI determinat de cele două drepte: - selectați pictograma 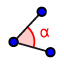 , apoi un punct de pe o latură a unghiului, vârful, apoi un punct de pe cealaltă latură, în ordine inversă mersului acelor de ceasornic.
, apoi un punct de pe o latură a unghiului, vârful, apoi un punct de pe cealaltă latură, în ordine inversă mersului acelor de ceasornic.
 , apoi dați click pe sufrafața de lucru a ferestrei GeoGebra de mai jos și introduceți raza 3 în fereastra ce apare pe pagina principală.
Ați realizat un cerc de centru A și rază 3.
2) Desenați patru PUNCTE (B, C, D și E) pe cercul de centru A, folosind pictograma
, apoi dați click pe sufrafața de lucru a ferestrei GeoGebra de mai jos și introduceți raza 3 în fereastra ce apare pe pagina principală.
Ați realizat un cerc de centru A și rază 3.
2) Desenați patru PUNCTE (B, C, D și E) pe cercul de centru A, folosind pictograma  .
3) Trasați două DREPTE determinate de cele patru puncte, astfel încât acestea să fie concurente într-un punct aflat în interiorul cercului: - Faceți acest lucru selectând pictograma
.
3) Trasați două DREPTE determinate de cele patru puncte, astfel încât acestea să fie concurente într-un punct aflat în interiorul cercului: - Faceți acest lucru selectând pictograma  , apoi selectați câte două dintre punctele de pe cerc.
4) Notați PUNCTUL DE INTERSECȚIE al celor două drepte: - selectați pictograma
, apoi selectați câte două dintre punctele de pe cerc.
4) Notați PUNCTUL DE INTERSECȚIE al celor două drepte: - selectați pictograma , apoi selectați cele două drepte concurente. Veți constata apariția unui punct F.
5) Aflați MĂSURA UNGHIULUI determinat de cele două drepte: - selectați pictograma
, apoi selectați cele două drepte concurente. Veți constata apariția unui punct F.
5) Aflați MĂSURA UNGHIULUI determinat de cele două drepte: - selectați pictograma  , apoi un punct de pe o latură a unghiului, vârful, apoi un punct de pe cealaltă latură, în ordine inversă mersului acelor de ceasornic.
, apoi un punct de pe o latură a unghiului, vârful, apoi un punct de pe cealaltă latură, în ordine inversă mersului acelor de ceasornic.Modificați poziția punctelor aflate pe cerc.
Ce observați odată cu modificarea poziției punctelor?
Măsura unghiului cu vârful în interiorul cercului
Știm că măsura unghiului cu vârful în interiorul cercului este egală cu semisuma măsurilor arcelor determinate de laturile acestuia pe cerc.
Pentru a verifica acest lucru cu ajutorul GeoGebra, mai întâi ne vom aminti că măsura unui arc de cerc este egală cu măsura unghiului la centru corespunzător acestuia.
În fereastra GeoGebra, vom crea SECTOARELE CIRCULARE corespunzătoare arcelor determinate de laturile unghiului cu vârful în interiorul cercului:
a) Selectați pictograma  b) Selectați centrul cercului (A), apoi capetele arcului de cerc, în ordine contrară sensului de mers ale acelor de ceasornic.
c) Repetați pasul b) pentru arcul opus.
d) Determinați măsurile unghiurilor la centru corespunzătoare sectoarelor circulare, ca la pasul 5).
b) Selectați centrul cercului (A), apoi capetele arcului de cerc, în ordine contrară sensului de mers ale acelor de ceasornic.
c) Repetați pasul b) pentru arcul opus.
d) Determinați măsurile unghiurilor la centru corespunzătoare sectoarelor circulare, ca la pasul 5).
 b) Selectați centrul cercului (A), apoi capetele arcului de cerc, în ordine contrară sensului de mers ale acelor de ceasornic.
c) Repetați pasul b) pentru arcul opus.
d) Determinați măsurile unghiurilor la centru corespunzătoare sectoarelor circulare, ca la pasul 5).
b) Selectați centrul cercului (A), apoi capetele arcului de cerc, în ordine contrară sensului de mers ale acelor de ceasornic.
c) Repetați pasul b) pentru arcul opus.
d) Determinați măsurile unghiurilor la centru corespunzătoare sectoarelor circulare, ca la pasul 5).Măsura unghiului cu vârful în interiorul cercului este egală cu semisuma măsurilor arcelor determinate de laturile acestuia pe cerc.
Verificați relația de mai sus folosind măsurile obținute în construcție.